Сумма квадратов чисел — такая задача с числом 365 представлена на картине художника Н. П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского», 1895 год.
Ученики 19 века пытаются решить непростую задачу в уме, без помощи подручных средств. Тогда счет в уме или устный счет назывался «умственный».

На картине учитель — Сергей Александрович Рачинский, который был биологом, профессором Московского университета, а потом круто изменил свою жизнь. Он основал народную школу для крестьянских детей в своем родовом поместье Татево в Смоленской губернии.
Рачинский придавал большое значение, в частности, устному счету. Его любимая фраза: «С поля за карандашом и бумагой не побежишь. Решать надо умственно».
Калькулятор умеет считать
Сейчас, когда у каждого из нас под рукой есть калькулятор (в компьютере, в телефоне, в часах и в других гаджетах), счет в уме уже не в почете. Зачем? Ведь можно посчитать на калькуляторе.
Однако, не будем торопиться. Чтобы решить любую задачу, нужно ЗНАТЬ, как ее решать? А что мы знаем? Мы знаем, например, как на калькуляторе умножить 10 на 10. Можем умножить 11 на 11, а также 12 на 12 и так далее.
Мы также знаем, что можно поместить во временную память калькулятора результаты подобных умножений – обычно это клавиша калькулятора M+.
Еще мы знаем, как извлечь из памяти результат сложения всех помещенных в нее данных – обычно это клавиша MR. И, наконец, мы умеем делить полученный результат на 365.
Похоже, что нам достаточно тех знаний, которые у нас есть, чтобы решить трудную задачу. Тем не менее, нужно проделать довольно большую работу, и главное, при этом ни разу не ошибиться, чтобы получить верный результат.
Задача на сумму квадратов чисел
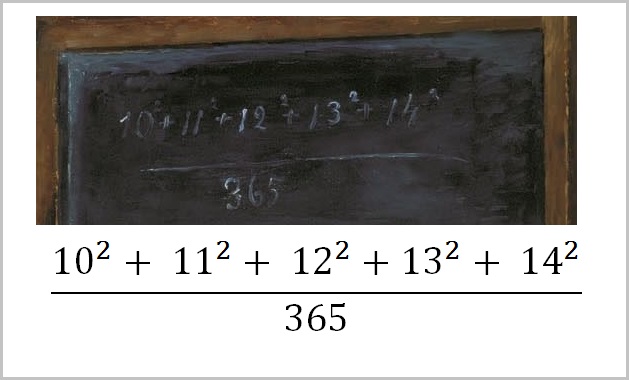
Как же иначе решить предложенную задачу, если не выполнить требуемые арифметические действия, например, на калькуляторе? – спросит любой современный человек. Оказывается можно иметь совсем другие знания – это знания о числах. Да, да. Есть такие знания о числах, которые помогают решить некоторые трудные задачи намного проще, чем даже на калькуляторе.
Именно так обстоит дело с числом 365. Это число хорошо нам известно, как число дней в обычном, не високосном году. Имея под рукой калькулятор, можно легко проверить, что число 365 есть сумма квадратов чисел 10, 11 и 12.
10*10 + 11*11 + 12*12 = 100 + 121 + 144 = 365
13*13 + 14*14 = 169 + 196 = 365
То есть, если умножить 10 само на себя, 11 умножить на 11 и 12 умножить на себя, то в сумме эти три числа дадут результат 365. Это мы можем просто знать, не используя никаких подручных средств для вычислений и даже не напрягая нашу память для проведения устного счета, счета в уме. В школе необходимо знать наизусть таблицу умножения. Также зачастую требуется выучить квадраты всех чисел от 1 до 25.
Сумма квадратов чисел 13 и 14
И вот, что интересно. Оказывается, число 365 получается также в результате сложения квадратов еще двух «соседних» чисел 13 и 14. То есть, если умножить 13 само на себя, 14 умножить на 14, а полученные числа сложить, то опять в сумме получим число 365. Налицо необычные свойства числа 365, о которых мы теперь ЗНАЕМ, не применяя вычислений.
10*10 + 11*11 + 12*12 = 365
13*13 + 14*14 = 365
(10*10 + 11*11 + 12*12) + (13*13 + 14*14) = 365 + 365 = 365 * 2
(365*2) / 365 = 2
Какой получается результат в «трудной задаче», приведенной на картине художника? Над дробью мы теперь отчетливо «видим» сумму двух чисел: 365 и 365! Под дробью стоит одно единственное число 365. Если же два слагаемые 365 и 365 разделить на одно число 365, то результат очевиден – это «двойка», то есть 2.
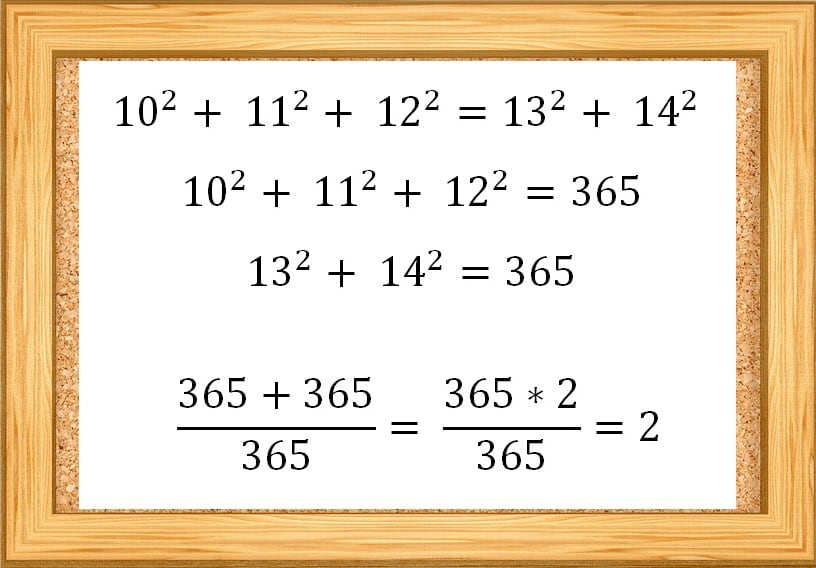
А Вы попробовали решить эту задачу на калькуляторе? Получился такой же ответ?!
Вот так, безо всякого калькулятора и без напряжения мысли во время устного счета, можно найти решение «трудной задачи», которая оказывается совсем не трудной для тех, кто знает об удивительных свойствах числа 365 – о числе дней в году.
Другая задача на сумму квадратов двух чисел
Сумма квадратов двух последовательных натуральных чисел равна 365. Найдите эти числа.
Последовательные числа — это те, которые идут по порядку, друг за другом. Например, пары чисел 13, 14 являются последовательными.
13*13 + 14*14 = 365
Ответ к последней задаче: числа 13 и 14. Сумма квадратов двух последовательных натуральных чисел 13 и 14 равна 365.






